我們用延續之前相對熵舉例裡的中二病吧
這次我們來看看 MLL 與相對熵的互動

假設我們現在想知道國中生罹患中二病的機率
抽查了 50 個班級，每班 10 個學生
結果如下：

假設每個學生罹患中二病的情況是獨立事件且罹患機率為 true_pi
假設我們所觀察的現象服從二項分配 (現在 n = 10)
則它的機率分配函數(pdf)為
表示機率為 pi 且 10 個學生中有 k 個學生罹患中二病的機率

然後畫出每個我們所猜測的機率 pi (在此我們畫出 0 ~ 1)
它所對應的 log likelihood 值
結果如下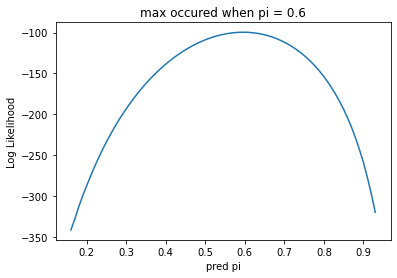

然後畫出每個我們所猜測的機率 pi (在此我們畫出 0 ~ 1)
它所對應的 KL散度值
結果如下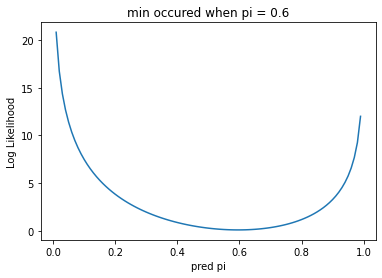

可以看到兩者最後的結果相同
只是在 LL 時，我們計算最大值
而在 KL 時，我們計算最小值

底下附上程式碼

import random
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import entropy
import math

# 選擇數的公式
def nCr(n, r):
    f = math.factorial
    return f(n) / f(r) / f(n-r)

# 二項分配
def binomial_distribution(n, k, pi):
    return nCr(n, k)*(pi**k)*(1-pi)**(n-k)
    
# 真實機率
true_pi = 0.587

# 創造樣本
sample = [sum(1 for i in range(10) if random.random()<true_pi) for j in range(50)]

# 依據觀察所得的機率值
prob_obs = [sample.count(i)/50 for i in range(11)]

# 計算 LL
def loglikelihood(pi, observed):
    '''
    observed : set of (xi,yi); n = xi, k = yi
    '''
    p_i = [np.round(binomial_distribution(n = obs[0], k = obs[1], pi = pi), 6) for obs in observed]
    
    # the domain of log is (0, inf) and log0 → -inf when base > 1
    return sum(math.log(p) if p!=0 else -np.inf for p in p_i)

# pi 的範圍必在 0 ~ 1
guess_pi = np.arange(0, 1, 0.01)

# 畫出每個 pi 所對應的 LL
observed = [[10,y] for y in sample]
LL = [loglikelihood(pi, observed) for pi in guess_pi]

plt.plot(guess_pi, LL)
plt.title('max occured when pi = '+str(np.round(guess_pi[LL.index(max(LL))], 2)))
plt.xlabel('pred pi')
plt.ylabel('Log Likelihood')
plt.show()


# 畫出每個 pi 所對應的 KL 散度
KL = [entropy(prob_obs, [binomial_distribution(10, k, pi) for k in range(11)]) for pi in guess_pi]

plt.plot(guess_pi, KL)
plt.title('min occured when pi = '+str(np.round(guess_pi[KL.index(min(KL))], 2)))
plt.xlabel('pred pi')
plt.ylabel('Log Likelihood')
plt.show()